Terinspirasi dari bahasa natural manusia, ilmuwan-ilmuwan ilmu komputer yang mengembangkan bahasa pemrograman turut serta memberikan tata bahasa (pemrograman) secara formal. Tata bahasa ini diciptakan secara bebas-konteks dan disebut CFG (Context Free Grammar). Hasilnya, dengan pendekatan formal ini, kompiler suatu bahasa pemrograman dapat dibuat lebih mudah dan menghindari ambiguitas ketika parsing bahasa tersebut. Contoh desain CFG untuk parser, misal : B -> BB | (B) | e untuk mengenali bahasa dengan hanya tanda kurung {‘(’,’)’} sebagai terminal-nya. Proses parsing adalah proses pembacaan untai dalam bahasa sesuai CFG tertentu, proses ini harus mematuhi aturan produksi dalam CFG tersebut. Secara formal, CFG didefinisikan[2] : CFG G = (V,T,P,S), dimana V adalah daftar variabel produksi T, adalah daftar simbol atau terminal yang dipakai dalam CFG P, adalah aturan produksi CFG S, adalah variabel start aturan produksi CFG dapat ‘dinormalkan’ dengan pola tersendiri supaya tidak ambigu dan lebih sederhana, meskipun normalisasi CFG kadang membuat aturan produksi menjadi lebih banyak dari sebelumnya. Teknik normalisasi yang digunakan dalam makalah ini adalah CNF (Chomsky Normal Form).
S -> aA | bB (1)
A-> Baa|ba
B -> bAA|ab
CFG (1) tersebut ekivalen dengan CFG dibawah ini,dimana symbol terminal memiliki
variabel produksi tersendiri:
S -> DA | EB (2)
A -> BDD | ED
B -> EAA | DE
D -> a
E -> b
CNF yang dihasilkan dari CFG (2) diatas ialah:
S -> DA | EB (3)
A -> BF | ED
B -> EH | DE
F -> DD
H -> AA
D -> a
E -> b
Setelah terbentuk CFG yang telah dinormalkan secara CNF, dalam implementasi parsing, terdapat algoritma yang berguna untuk menentukan apakah suatu untai ‘valid’, atau dapat diciptakan dari aturan-aturan CFG yang ada. Salah satu algoritma yang dapat dipakai adalah Algoritma Cocke-Younger-Kasami (CYK). Algoritma ini menyelesaikan masalah analisa kembali sebuah sub-untai yang sama karena seharusnya analisa sub-untai independen terhadap parsing sub-untai yang diparsing setelahnya. Dengan Program Dinamis, independensi yang diinginkan dapat dicapai ketika parsing. Algoritma CYK termasuk dalam bidang Program Dinamis karena algoritma ini membangun tabel status dua dimensi ketika parsing dimana penentuan parsing selanjutnya diturunkan atau dihasilkan
dari parsing sebelumnya, hingga akhir untai. Selain untuk mengetahui validitas untai dalam suatu CFG, algoritma CYK yang dimodifikasi dapat dipergunakan pula untuk membangun pohon parsing.
Contoh 1 :
Diketahui grammar G1 = {I ® H½I H½IA, H ® a½b½c½...½z, A ® 0½1½2½...½9}
dengan I adalah simbol awal. Berikut ini kedua cara analisa sintaks untuk kalimat x23b.
cara 1 (derivasi) cara 2 (parsing)
I IH
IAH
IAAH
HAAH
xAAH
x2AH
x23H
x23b
Sebuah kalimat dapat saja mempunyai lebih dari satu pohon.
Contoh 2 :
Diketahui grammar G 2 = {S ® SOS½A , O ® *½+, A ® 0½1½2½...½9}
Kalimat : 2*3+7 mempunyai dua pohon sintaks berikut :
Sebuah kalimat yang mempunyai lebih dari satu pohon sintaks disebut kalimat ambigu
(ambiguous). Grammar yang menghasilkan paling sedikit sebuah kalimat ambigu disebut
grammar ambigu.
5.2 Push Down Automata (PDA)
PDA adalah mesin otomata dari TBBK yang diimplementasikan dengan stack
sehingga hanya terdapat operasi “push” dan “pop” Stack (tumpukan) adalah suatu struktur
data yang menggunakan prinsip LIFO (Last In First Out). Sebuah stack selalu memiliki top
of stack dan elemen-elemen stack itu yang akan masuk ke dalam stack dengan method
“push” dan akan keluar dari stack dengan method “pop”.
• Definisi : PDA adalah pasangan 7 tuple M = (Q, S, G, q 0 , Z0 , d, A), dimana : Q : himpunan hingga stata, S : alfabet input, G : alfabet stack, q 0 Î Q : stata awal, Z0 Î G : simbol awal stack, A Í Q : himpunan stata penerima, fungsi transisi d : Q × (S È {e}) × G ® 2 Q ×G* (himpunan bagian dari Q × G*)
• Untuk stata q Î Q, simbol input a Î S, dan simbol stack XÎ G, d(q, a, X) = (p, a)
berarti : PDA bertransisi ke stata p dan mengganti X pada stack dengan string a.
• Konfigurasi PDA pada suatu saat dinyatakan sebagai triple (q, x, a), dimana :
q Î Q : stata pada saat tersebut, x Î S* : bagian string input yang belum dibaca, dan a
Î G* : string yang menyatakan isi stack dengan karakter terkiri menyatakan top of
stack.
• Misalkan (p, ay, Xb) adalah sebuah konfigurasi, dimana : a Î S, y Î S*, X Î G, dan b
Î G*. Misalkan pula d(p, a, X) = (q, g) untuk q Î Q dan g Î G*. Dapat kita tuliskan
bahwa : (p, ay, Xb) (q, y, gb).
Sebuah PDA dinyatakan dengan :
Q = himpunan state
= himpunan simbol input
T = simbol stack
= fungsi transisi
S = state awal
F = state akhir
Z = top of stack
PDA memiliki 2 jenis transisi, yaitu yang merima simbol input, simbol top of stack, dan state. Setiap pilihan terdiri dari state berikutnya dan simbol- simbol. Penggantian isi stack dilakukan dengan opersi push dan pop. Jenis transisi yang kedua adalah transisi . Transisi tidak melakukan pembacaan input namun hanya menerima simbol top of stack dan state. Transisi ini memungkinkan PDA untuk memanipulasi isi stack dan berpindah antar state tanpa membaca input.
Contoh 14 (PDA Deterministik):
PDA M = (Q, S, G, q 0 , Z 0 , d, A) pengenal palindrome L = {xcx T½x Î (a½b)*}, dimana x T adalah cermin(x), mempunyai tuple : Q = {q 0 , q 1 , q 2 }, A = { q 2 }, S = {a, b, c}, G = {a, b, Z0 }, dan fungsi transisi d terdefinisi melalui tabel berikut : Sebagai contoh, perhatikan bahwa fungsi transisi No. 1 dapat dinyatakan sebagai : d(q 0 , a, Z0 ) = (q 0 , aZ 0 ). Pada tabel transisi tersebut terlihat bahwa pada stata q 0 PDA akan melakukan PUSH jika mendapat input a atau b dan melakukan transisi stata ke stata q 1 jika mendapat input c. Pada stata q1 PDA akan melakukan POP.
Berikut ini pengenalan dua string oleh PDA di atas :
1. abcba : (q 0 , abcba, Z 0 ) (q 0 , bcba, aZ 0 ) (1)
(q 0 , cba, baZ 0 ) (4)
(q1 , ba, baZ 0 ) (9)
(q1 , a, aZ 0 ) (11)
(q1 , e, Z 0 ) (10)
(q 2 , e, Z 0 ) (12) (diterima)
2. acb : (q 0 , acb, Z 0 ) (q 0 , cb, aZ 0 ) (1)
(q1 , b, aZ0 ) (8), (crash ® ditolak)
3. ab : (q 0 , ab, Z 0 ) (q 0 , b, aZ0 ) (1)
(q 0 , e, baZ0 ) (4) (crash ® ditolak)
Penerimaan dan penolakan tiga string di atas dapat dijelaskan sebagai berikut :
1. string abcba diterima karena tracing sampai di stata penerima (q 2 ) dan string “abcba”
selesai dibaca (string yang belum dibaca = e)
2. string acb ditolak karena konfigurasi akhir (q 1 , b, a Z 0 ) sedangkan fungsi transisi
d(q 1 , b, a) tidak terdefinsi
3. string ab ditolak karena konfigurasi akhir (q 0 , e, baZ0 ) sedangkan fungsi transisi d(q 0 ,
e, b) tidak terdefinsi
Ilustrasi graf fungsi transisi PDA di atas ditunjukkan melalui gambar berikut :
• Notasi (p, ay, Xb) (q, y, gb) dapat diperluas menjadi : (p, x, a) * (q, y, b), yang
berarti konfigurasi (q, y, b) dicapai melalui sejumlah (0 atau lebih) transisi.
• Ada dua cara penerimaan sebuah kalimat oleh PDA, yang masing-masing terlihat dari
konfigurasi akhir, sebagaimana penjelasan berikut :
Jika M = (Q, S, G, q 0 , Z 0 , d, A) adalah PDA dan x ÎS*, maka x diterima dengan stata
akhir (accepted by final state) oleh PDA M jika : (q 0 , x, Z0 ) * (q, e, a) untuk a Î G
* dan q Î A. x diterima dengan stack hampa (accepted by empty stack) oleh PDA M
jika : (q 0 , x, Z0 ) * (q, e, e) untuk q Î Q.
Contoh 15 (PDA Non-Deterministik):
PDA M = (Q, S, G, q 0 , Z0 , d, A) pengenal palindrome L = {xx T ½x Î (a½b)*} mempunyai
komponen tuple berikut : Q = {q 0 , q1 , q 2 }, A = { q 2 }, S = {a, b}, G = {a, b, Z0 },
dan fungsi transisi d terdefinisi melalui tabel berikut :
Pada tabel transisi tersebut terlihat bahwa pada stata q 0 PDA akan melakukan PUSH jika
mendapat input a atau b dan melakukan transisi stata ke stata q 1 jika mendapat input e.
Pada stata q 1 PDA akan melakukan POP. Contoh 14 dan 15 menunjukkan bahwa PDA
dapat dinyatakan sebagai mesin PUSH-POP.
Berikut ini pengenalan string “baab” oleh PDA di atas :
1. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q1 , ab, abZ 0 ) (3 kanan)
(q1 , b, bZ0 ) (11)
(q1 , e, Z 0 ) (10)
(q 2 , e, Z 0 ) (12) (diterima)
2. (q 0 , baab, Z 0 ) (q1 , baab, Z 0 ) (2 kanan) (crash ® ditolak)
3. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q 0 , b, aabZ 0 ) (3 kiri)
(q1 , b, aabZ 0 ) (4 kanan) (crash ® ditolak)
4. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q 0 , b, aabZ 0 ) (3 kiri)
(q 0 , e, baabZ 0 ) (4 kiri)
(q1 , e, baabZ 0 ) (9) (crash ® ditolak)
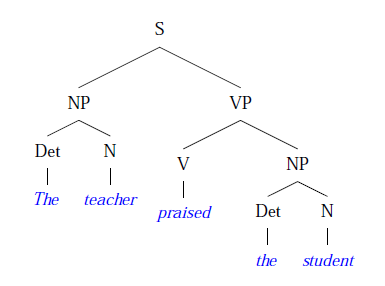
Gambar 5.1. Gambaran parsing bahasa natural (Inggris)
Contoh desain CNF dari bahasa CFG, semisal CFGberikut:S -> aA | bB (1)
A-> Baa|ba
B -> bAA|ab
CFG (1) tersebut ekivalen dengan CFG dibawah ini,dimana symbol terminal memiliki
variabel produksi tersendiri:
S -> DA | EB (2)
A -> BDD | ED
B -> EAA | DE
D -> a
E -> b
CNF yang dihasilkan dari CFG (2) diatas ialah:
S -> DA | EB (3)
A -> BF | ED
B -> EH | DE
F -> DD
H -> AA
D -> a
E -> b
Setelah terbentuk CFG yang telah dinormalkan secara CNF, dalam implementasi parsing, terdapat algoritma yang berguna untuk menentukan apakah suatu untai ‘valid’, atau dapat diciptakan dari aturan-aturan CFG yang ada. Salah satu algoritma yang dapat dipakai adalah Algoritma Cocke-Younger-Kasami (CYK). Algoritma ini menyelesaikan masalah analisa kembali sebuah sub-untai yang sama karena seharusnya analisa sub-untai independen terhadap parsing sub-untai yang diparsing setelahnya. Dengan Program Dinamis, independensi yang diinginkan dapat dicapai ketika parsing. Algoritma CYK termasuk dalam bidang Program Dinamis karena algoritma ini membangun tabel status dua dimensi ketika parsing dimana penentuan parsing selanjutnya diturunkan atau dihasilkan
dari parsing sebelumnya, hingga akhir untai. Selain untuk mengetahui validitas untai dalam suatu CFG, algoritma CYK yang dimodifikasi dapat dipergunakan pula untuk membangun pohon parsing.
Gambar 5.2 Pohon parsing yang terbentuk dari sebuah bahasa natural
Contoh 1 :
Diketahui grammar G1 = {I ® H½I H½IA, H ® a½b½c½...½z, A ® 0½1½2½...½9}
dengan I adalah simbol awal. Berikut ini kedua cara analisa sintaks untuk kalimat x23b.
cara 1 (derivasi) cara 2 (parsing)
I IH
IAH
IAAH
HAAH
xAAH
x2AH
x23H
x23b
Sebuah kalimat dapat saja mempunyai lebih dari satu pohon.
Contoh 2 :
Diketahui grammar G 2 = {S ® SOS½A , O ® *½+, A ® 0½1½2½...½9}
Kalimat : 2*3+7 mempunyai dua pohon sintaks berikut :
Sebuah kalimat yang mempunyai lebih dari satu pohon sintaks disebut kalimat ambigu
(ambiguous). Grammar yang menghasilkan paling sedikit sebuah kalimat ambigu disebut
grammar ambigu.
5.2 Push Down Automata (PDA)
PDA adalah mesin otomata dari TBBK yang diimplementasikan dengan stack
sehingga hanya terdapat operasi “push” dan “pop” Stack (tumpukan) adalah suatu struktur
data yang menggunakan prinsip LIFO (Last In First Out). Sebuah stack selalu memiliki top
of stack dan elemen-elemen stack itu yang akan masuk ke dalam stack dengan method
“push” dan akan keluar dari stack dengan method “pop”.
• Definisi : PDA adalah pasangan 7 tuple M = (Q, S, G, q 0 , Z0 , d, A), dimana : Q : himpunan hingga stata, S : alfabet input, G : alfabet stack, q 0 Î Q : stata awal, Z0 Î G : simbol awal stack, A Í Q : himpunan stata penerima, fungsi transisi d : Q × (S È {e}) × G ® 2 Q ×G* (himpunan bagian dari Q × G*)
• Untuk stata q Î Q, simbol input a Î S, dan simbol stack XÎ G, d(q, a, X) = (p, a)
berarti : PDA bertransisi ke stata p dan mengganti X pada stack dengan string a.
• Konfigurasi PDA pada suatu saat dinyatakan sebagai triple (q, x, a), dimana :
q Î Q : stata pada saat tersebut, x Î S* : bagian string input yang belum dibaca, dan a
Î G* : string yang menyatakan isi stack dengan karakter terkiri menyatakan top of
stack.
• Misalkan (p, ay, Xb) adalah sebuah konfigurasi, dimana : a Î S, y Î S*, X Î G, dan b
Î G*. Misalkan pula d(p, a, X) = (q, g) untuk q Î Q dan g Î G*. Dapat kita tuliskan
bahwa : (p, ay, Xb) (q, y, gb).
Sebuah PDA dinyatakan dengan :
Q = himpunan state
= himpunan simbol input
T = simbol stack
= fungsi transisi
S = state awal
F = state akhir
Z = top of stack
PDA memiliki 2 jenis transisi, yaitu yang merima simbol input, simbol top of stack, dan state. Setiap pilihan terdiri dari state berikutnya dan simbol- simbol. Penggantian isi stack dilakukan dengan opersi push dan pop. Jenis transisi yang kedua adalah transisi . Transisi tidak melakukan pembacaan input namun hanya menerima simbol top of stack dan state. Transisi ini memungkinkan PDA untuk memanipulasi isi stack dan berpindah antar state tanpa membaca input.
Contoh 14 (PDA Deterministik):
PDA M = (Q, S, G, q 0 , Z 0 , d, A) pengenal palindrome L = {xcx T½x Î (a½b)*}, dimana x T adalah cermin(x), mempunyai tuple : Q = {q 0 , q 1 , q 2 }, A = { q 2 }, S = {a, b, c}, G = {a, b, Z0 }, dan fungsi transisi d terdefinisi melalui tabel berikut : Sebagai contoh, perhatikan bahwa fungsi transisi No. 1 dapat dinyatakan sebagai : d(q 0 , a, Z0 ) = (q 0 , aZ 0 ). Pada tabel transisi tersebut terlihat bahwa pada stata q 0 PDA akan melakukan PUSH jika mendapat input a atau b dan melakukan transisi stata ke stata q 1 jika mendapat input c. Pada stata q1 PDA akan melakukan POP.
Berikut ini pengenalan dua string oleh PDA di atas :
1. abcba : (q 0 , abcba, Z 0 ) (q 0 , bcba, aZ 0 ) (1)
(q 0 , cba, baZ 0 ) (4)
(q1 , ba, baZ 0 ) (9)
(q1 , a, aZ 0 ) (11)
(q1 , e, Z 0 ) (10)
(q 2 , e, Z 0 ) (12) (diterima)
2. acb : (q 0 , acb, Z 0 ) (q 0 , cb, aZ 0 ) (1)
(q1 , b, aZ0 ) (8), (crash ® ditolak)
3. ab : (q 0 , ab, Z 0 ) (q 0 , b, aZ0 ) (1)
(q 0 , e, baZ0 ) (4) (crash ® ditolak)
Penerimaan dan penolakan tiga string di atas dapat dijelaskan sebagai berikut :
1. string abcba diterima karena tracing sampai di stata penerima (q 2 ) dan string “abcba”
selesai dibaca (string yang belum dibaca = e)
2. string acb ditolak karena konfigurasi akhir (q 1 , b, a Z 0 ) sedangkan fungsi transisi
d(q 1 , b, a) tidak terdefinsi
3. string ab ditolak karena konfigurasi akhir (q 0 , e, baZ0 ) sedangkan fungsi transisi d(q 0 ,
e, b) tidak terdefinsi
Ilustrasi graf fungsi transisi PDA di atas ditunjukkan melalui gambar berikut :
• Notasi (p, ay, Xb) (q, y, gb) dapat diperluas menjadi : (p, x, a) * (q, y, b), yang
berarti konfigurasi (q, y, b) dicapai melalui sejumlah (0 atau lebih) transisi.
• Ada dua cara penerimaan sebuah kalimat oleh PDA, yang masing-masing terlihat dari
konfigurasi akhir, sebagaimana penjelasan berikut :
Jika M = (Q, S, G, q 0 , Z 0 , d, A) adalah PDA dan x ÎS*, maka x diterima dengan stata
akhir (accepted by final state) oleh PDA M jika : (q 0 , x, Z0 ) * (q, e, a) untuk a Î G
* dan q Î A. x diterima dengan stack hampa (accepted by empty stack) oleh PDA M
jika : (q 0 , x, Z0 ) * (q, e, e) untuk q Î Q.
Contoh 15 (PDA Non-Deterministik):
PDA M = (Q, S, G, q 0 , Z0 , d, A) pengenal palindrome L = {xx T ½x Î (a½b)*} mempunyai
komponen tuple berikut : Q = {q 0 , q1 , q 2 }, A = { q 2 }, S = {a, b}, G = {a, b, Z0 },
dan fungsi transisi d terdefinisi melalui tabel berikut :
Pada tabel transisi tersebut terlihat bahwa pada stata q 0 PDA akan melakukan PUSH jika
mendapat input a atau b dan melakukan transisi stata ke stata q 1 jika mendapat input e.
Pada stata q 1 PDA akan melakukan POP. Contoh 14 dan 15 menunjukkan bahwa PDA
dapat dinyatakan sebagai mesin PUSH-POP.
Berikut ini pengenalan string “baab” oleh PDA di atas :
1. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q1 , ab, abZ 0 ) (3 kanan)
(q1 , b, bZ0 ) (11)
(q1 , e, Z 0 ) (10)
(q 2 , e, Z 0 ) (12) (diterima)
2. (q 0 , baab, Z 0 ) (q1 , baab, Z 0 ) (2 kanan) (crash ® ditolak)
3. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q 0 , b, aabZ 0 ) (3 kiri)
(q1 , b, aabZ 0 ) (4 kanan) (crash ® ditolak)
4. (q 0 , baab, Z 0 ) (q 0 , aab, bZ 0 ) (2 kiri)
(q 0 , ab, abZ 0 ) (5 kiri)
(q 0 , b, aabZ 0 ) (3 kiri)
(q 0 , e, baabZ 0 ) (4 kiri)
(q1 , e, baabZ 0 ) (9) (crash ® ditolak)


No comments:
Post a Comment